Otázka 1 (H): Uveďte nejvýznamnější Archimédovy spisy, které se nacházejí v tzv. Archimédově kodexu
O rovnováze rovinných útvarů, O plovoucích tělesech I, II, Metoda, O spirálách, O kouli a válci I, II, Měření kruhu, Stomachion.
Otázka 2 (H): Čím se zabývá spis Metoda? Uveďte několik konkrétních výsledků
Obsahy a objemy útvarů vzniklých z kuželoseček. Konkrétněji objem rotačního elipsoidu. Těžiště úseče rotačního paraboloidu.
Otázka 3 (O): Určete objem úseče tělesa ohraničeného rotačním paraboloidem a rovinou kolmou k jeho ose pomocí Archimédovy metody
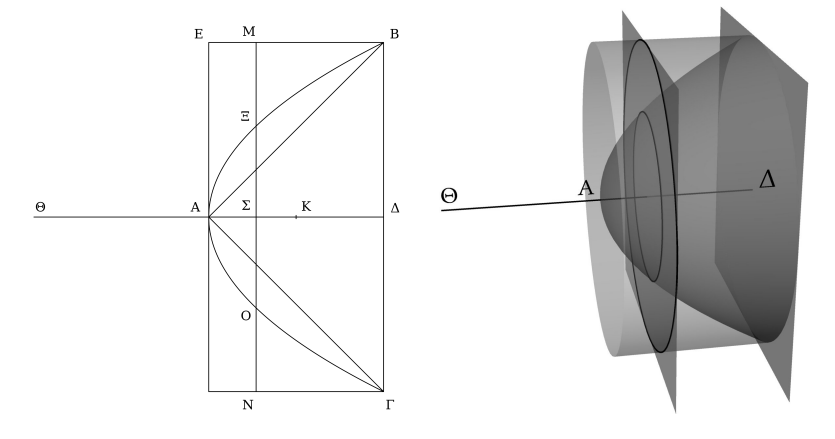
a , proto .
kruh v paraboloidu kruh ve válci.
Válec na místě (v K) vyváží paraboloid v .
Tedy je těleso v rovnováze a platí, že objem paraboloidu je polovina opsaného válce.
Otázka 4 (O): Určete těžiště úseče tělesa ohraničeného rotačním paraboloidem a rovinou kolmou k jeho ose pomocí Archimédovy metody
Užijeme předchozí nákres.
Z toho plyne, že:
Z toho vyplývá, že těžiště je ve dvou třetinách parabolické úseče.
Otázka 5 (O): Určete objem koule pomocí Archimédovy metody.
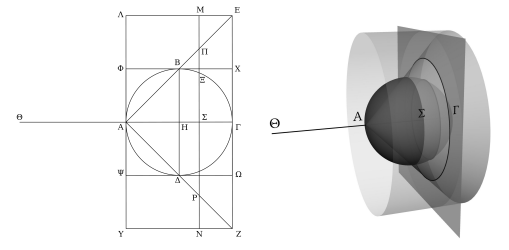
Jelikož , pak platí, že
Jelikož se válec objemem rovná objem válci opsanému dané kouli, a to 24 vepsaným kuželům, pak platí, že koule je rovna 4 vepsaným kuželům. Z toh plyne, že objem koule je .
Otázka 6 (H): O čem pojednává spis Stomachion?
O řecké skládačce a o tom, že některé části mají rozdílné úhly apod.
Otázka 7 (O): Stručně naznačte školské odvození vztahu pro objem koule pomocí Cavalieriho principu.
Mějme polokouli o poloměru a válec s vyřízlým kuželem o poloměru a výšce . Plocha řezu kolmého na výšku je nějaký kruh, přičemž platí, že . Z toho plyne, že jeho obsah je . Obsah řezu druhého tělesa je roven obsahu mezikruží o obsahu . Tedy dle Cavalieriho principu mají obě tělesa stejný objem. Z toho vyplývá, že objem polokoule je roven a tedy, že příslušná koule má objem , což je hledaný vztah.
Otázka 8 (V): Jak vznikl název funkce sinus, kosinus?
Původní jméno sinu je jya, tedy polovina tětivy. Arabové to přejali jako jiba, poté změněno na jaib, tedy záliv. Následně to bylo přeloženo jako sinus v latině.
Kosinus je komplementární funkcí sinu, tedy proto předpona ko-.
Otázka 9 (V): Stručně vysvětlete, jak vytvořil Ptolemaios svou tabulku délek tětiv
Odvodil velikost a . Následně pomocí součtových vzorců určil . Poté provedl aproximaci k určení . Potom sestrojil všechny náslobky do a přičemž udělal pro každou hodnotu, čímž zamezil komulaci chyby vzniklé aproximací.
Otázka 10 (OV): Inspirujte se Ptolemaiovým postupem vytvoření tabulky délek tětiv a vyjádřete cos 15° pomocí známé hodnoty cos 30°. Postupujte jednoduše: tak, jak byste postupovali ve škole na tabuli, tj. odvoďte ze vzorce pro cos 2α vzorec pro cos α/2 (vyjádření pomocí cos α) a dosaďte hodnotu cos 30° (tu také odvoďte).
Nejprve odvodíme vztah pro polovinu úhlu:
Nyní se podíváme na . Podívejme se do rovnostranného trojúhelníku. V něm platí, že každý úhel má . Když spustíme výšku, tak u vrcholu bude úhel . Pokud má trojúhelník délku stran , pak platí, že . Pokud dosadíme do vzorce výše, dostaneme:
Otázka 11 (V): Vysvětlete, jakým způsobem Árjabhata zakódoval tabulku hodnot funkce sinus do dvou řádků své básně.
Rozdělil kružnici na 21600 dílků, přičemž jeden dílek odpovídá naší jedné minutě. První kvadrant rozdělil na 24 dílků. První hodnota odpovídá velikosti sinu jednoho dílku. Každý následující odpovídá velikosti sinu n-tého dílku minus sinus (n-1)-tého dílku.
Otázka 12 (OV): Jak vypočítal al-Káší hodnotu sin 1°? Odvoďte jeho postup.
Al-Káší vychází ze známého vzorce . Přičemž , címž dostává , z čehož udělá iterační předpis a . Pokračoval tak dlouho, dokud neměl požadovanou přesnost.
Otázka 13 (O): Stručně shrňte podstatu algoritmu CORDIC. Kdo a kdy jej objevil?
Algoritmus vznikl roku 1959, kdy jej vymyslel Jack Volder. CORDIC je založený na součtovém vzorce pro tangens. V paměti máme uloženy hodnoty úhlů, pro které platí, že . Hledaný úhel si pak napíšeme jako ciferný součet. Výsledek je pak:
Použijeme součtový vzorec pro tangens:
Když a , tak dostaneme, že , . Úplně na závěr to podělíme a dostaneme hledaný výsledek.
Otázka 14 (V): Řešení jakých otázek vedlo k objevu goniometrie?
Primárně se jedná o problémy astronomie, konkrétně o pohyby planet po obloze. V dobách starověkého Egypta se také kvůli stavbě pyramid řešil jejich sklon.
Otázka 15 (H): Co je excentr? Co je deferent a epicykl?
Mějme model obíhání Slunce kolem Země. Excentr je oběžná dráha, kdy střed obíhání je mimo střed Země. Druhý model kombinuje hlavní kružnici se středem ve středu Země (deferent) s menší kružnicí, kolem které Slunce obíhá (epicykl).
Otázka 16 (V): Stručně vysvětlete základní princip, na němž byly založeny první tabulky logaritmů, vysvětlete také volbu základů blízkých 1.
Bylo to prosté přiřazování přirozených čísel k jejich logaritmům o vhodném základě.
Volíme základ blízký jedné, aby byla tabulka dostatečně hustá. V případě volby většího exponentu bude tabulka řídká, jelikož posloupnost brzy začne velmi rychle růst. Z podobného důvodu volíme také základ menší než jedna.
Otázka 17 (V): Jak počítal Napier tabulky logaritmů?
Zvolil základ . Aby si ulehčil práci, všiml si, že se výsledné hodnoty od sebe příliš neliší, že vlastně vypadají, jako by to bylo linární a že chyba je řádově zanedbatelná. Tudíž jen psal lineární posloupnost a kontroloval, zda mu někde nenarůstá příliš velká chyba.
Otázka 18 (O): Odvoďte postup výpočtu ln 3 pomocí odmocnin.
Napišme a . Z definice platí . Na tento tvar aplikujeme n-tou odmocninu:
Z toho plyne, že
Z toho vyvodíme, že . Pomocí tohoto tvaru již můžeme aproximovat daný logaritmus.
(OV): Proč je logaritmus o základu e přirozený?
Z výpočtu výše plyne, že výpočet logaritmů o základu je jednoduchý, jelikož neobsahuje žádné dělení, které by logaritmy o jiných základech obsahovaly. Algoritmus na rychlé odmocňování je znám již ze starověkého Babylonu a násobení je velmi snadná operace. Pro tuto vlastnost je tudíž “přirozený”.
Otázka 19 (V): Vysvětlete původ slova logaritmus a jak je v něm obsažena matematická podstata logaritmů.
Vychází ze slov logos a arithmos. První označuje slovo poměr a vyjadřuje geometrickou posloupnost. To druhé vyjadřuje zase aritmetickou posloupnost. Tedy logaritmus je zobrazení z množiny členů geometrické posloupnosti do množiny členů posloupnosti aritmetické.
Otázka 20 (H): Co mohlo vést ke zkoumání kuželoseček? Uveďte jeden problém z praxe a jeden matematický problém.
Sluneční hodiny a jejich rozumná konstrukce, problém zdvojení krychle.
Otázka 21 (V): Na základě čeho nazval Apollónios parabolu? Ve kterém spisu to provedl?
Název vychází ze zadání úlohy z Euklidových Základů, kdy k danému čtverci hledáme odpovádající obdélník se stranou délky . Tedy . Řekové tomu říkali přikládání plochy, řecky paraballó. Z toho Apollónios odvodil název parabola ve své knize Kuželosečky.
Otázka 22 (O): Jak Apollónios odvodil charakteristickou vlastnost (dnes bychom řekli rovnici) paraboly jako řezu kuželové plochy, na jejímž základě ji také pojmenoval?
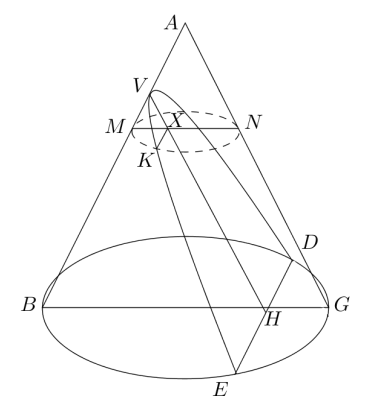
Z Thalétovy kružnice plyne, že . Jelikož je řez rovnoběžný s přímkou , tak . Z podobnosti trojuhelníků a plyne . Proto:
Nyní konstantu označíme jako a také a . Tedy dostaneme hledaný vztah .
Otázka 23 (O): S užitím analytické geometrie ukažte, proč se elipsa nazývá elipsa. Kdo a kdy zavedl tento název?
Nyní uděláme substituci , po níž se dostaneme k tvaru:
Tento tvar naznačuje, že zde něco “chybí”, tedy že od daného obdélníku odečítáme nějaký útvar. Odtud také název elipsa. Takto ji nazval Apollonios z Pergy ve svých Kuželosečkách na konci 3. stol. př. n. l.
Otázka 24 (H): Kdo a přibližně kdy napsal první text, z něhož se nám dochovaly významné pasáže, v nichž se pracuje s kuželosečkami?
První práce s kuželosečkami se nám dochovala v zlomcích spisů Řeka jménem Menaichmos ve 4. stol. př. n. l.
Otázka 25 (O): Naznačte podstatu Avicennovy konstrukce paraboly
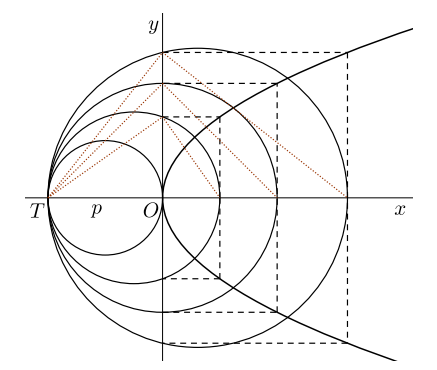
Dle Euklidovy věty víme, že . Zde platí, že pro každou jednu kružnici s průměrem minimálně platí, že , což je rovnice paraboly.
Otázka 26 (O): Jak definoval hyperbolu Menaichmos?
Menaichmos hyperbolu definuje jako křivku v rovině, pro jejíž body platí, že součin vzdáleností od dvou různoběžek je konstantní.
(V): Jak jeho definice souvisí s nepřímou úměrností?
Tvar se dá snadno převést na , což je nepřímá úměrnost mezi a .
(O): Ukažte, že grafem nepřímé úměrnosti je hyperbola (neboli ukažte, že Menaichmova definice hyperboly skutečně charakterizuje hyperbolu).
Převedeme do jiné báze tedy , . Nyní dostaneme . Po úpravě dostaneme , což rovnice paraboly.
Otázka 27 (V): Vysvětlete, co je zákon homogenity, kdo jej odstranil a jakým způsobem.
Zákon tvrdí, že nelze poměřovat navzájem různé veličiny, např. objem a obsah. Podle Řeků takové věci neměly v geometrii interpretaci, tudíž byly nepřípustné. Stejně tak bylo problematické povolit polynom stupně vyššího než tři. Odstranil jej Descartes, když prohlásil, že když je třeba dát do poměru objekty stejné dimenze, tak si prostě přikreslíme jedničku.
Otázka 28 (V): Používal R. Descartes kartézskou soustavu souřadnic? Měl dvě na sebe kolmé osy se stejnou jednotkou na každé z nich?
Používal trochu jiný systém. Měl pouze jednu osu, od které počítal vzdálenost. Až později byla přidána druhá kolmá osa.
Otázka 29 (V): Jak vznikl název matematické analýzy, přesněji: proč analýza?
Původně to označovalo cokoliv, kde se neznámá veličina nějak označila a pracovalo se s ní, jako bychom ji znali. Tento název se používal pro algebru. Vlivem Newtona se označení přeneslo i na infinitezimální počet. Později v 18. a 19. století se toto označení začalo používat pouze dnešním způsobem.
